4. Sinewaves

Brackeys video: Sinewaves

Sine and cosine

• Script reference: Mathf.Sin
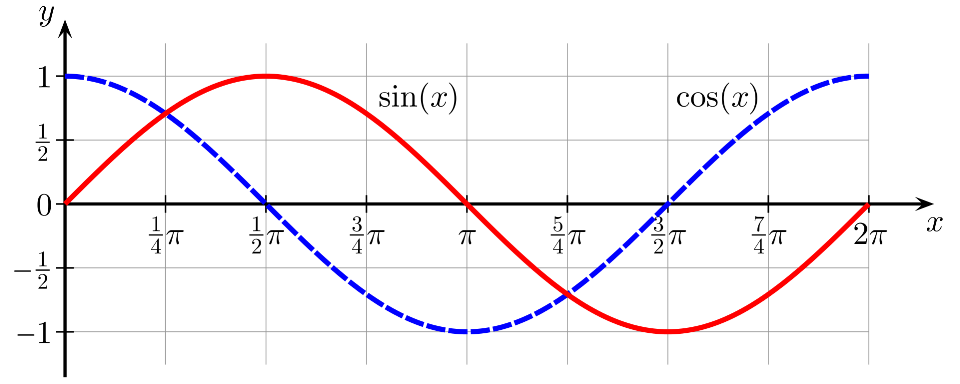
• $\sin(x)$ and $\cos(x)$ are oscillating functions that return a value between $1$ and $-1$
  • here, $x$ is an angle measured in radians (rad).
• Their form is the same, but $\cos$ is shifted from $\sin$ by $\pi/2$ rad: $\sin(x + \pi/2) = \cos(x)$

Degrees vs. radians

xx

Sin & Cos triangle definition

xx

Circular motion

xx

Extra: Polar coordinates

• Wikipedia: Polar coordinate system
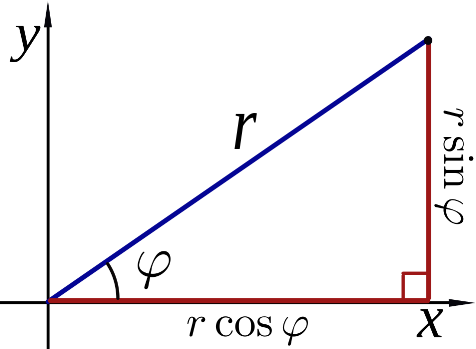
• Any two-dimensional vector $\vec{r} = (x,y)$ can be represented by its length $r$ and rotation angle $\varphi$ $x = r \cos{\varphi}$ $y = r \sin{\varphi}$

Code example

double phi = Mathf.pi/2;
double r = 5.0f;

Vector2 vec = new Vector2(
    r * Mathf.Cos(phi),
    r * Mathf.Sin(phi)
);

From cartesian ($x$ and $y$) to polar coordinates ($r$ and $\varphi$)

• What about the other way around? $r = \sqrt{x^2 + y^2}$ $\varphi = \mathrm{atan2}(y,x)$
  • $\mathrm{atan2}$ is an important function in game development
  • Script Reference: Mathf.Atan2
• In code:

    Vector2 vec = new Vector2(4.0f, 2,0f);
  
    double r = vec.Magnitude;
    double phi = Mathf.Atan2(vec.y, vec.x);