Math 3. Interpolation

3. Interpolation

Lerp

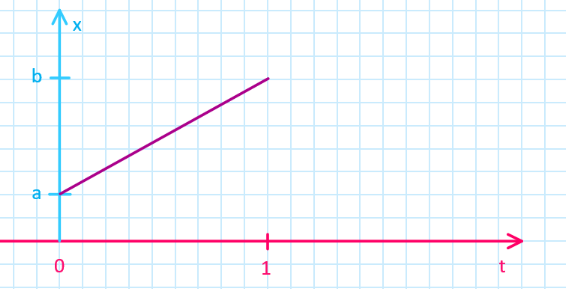
width:500px

  • “Lerp”, or linear interpolation, is a commonly used function in gamedev
    • returns the value $x$, which goes from $a$ to $b$, when $t$ goes from $0$ to $1$
    • when $t = 0$, $x = a$
    • when $t = 0.5$, $x = (b - a) / 2$ (“halfway”)
    • when $t = 1$, $x = b$
  • In Unity, the most basic lerp function isMathf.Lerp(a, b, t)

Lerp example

float x1 = Mathf.Lerp(5.0f, 15.0f, 0f);   // returns 5.0f
float x2 = Mathf.Lerp(5.0f, 15.0f, 0.5f); // returns 10.0f
float x3 = Mathf.Lerp(5.0f, 15.0f, 1.0f); // returns 15.0f

Note about Clamping

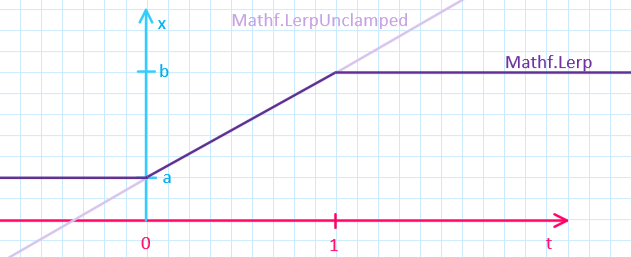
  • what if t is smaller than 0 or larger than 1?
  • Unity’s Mathf.Lerp is clamps the returned value automatically
    • $x$ is $a$ at minimum and $b$ at maximum
  • with Mathf.LerpUnclamped, the value is extrapolated when outside the limits!

Lerping different data types

  • Some data types are more complicated than just one float value
  • You can of course lerp every number value individually
  • Other way around: some types have their own built-in lerps
  • Unclamped versions exist, too.

Lerp practical example

  • Lerping usually happens in some sort of an update function, where we can use lerp to slowly change a value from a to b, while time moves forward. 
    [SerializeField] Transform endTransform;
[SerializeField] float lerpDuration;
Vector3 startPosition;
float startTime;
bool lerping = false;

void StartLerp() {
    startTime = Time.time;
    lerping = true;
}

void UpdateLerp() {
    if (!lerping) return
    float time = (Time.time - startTime) / lerpDuration;
    transform.position = Vector3.Lerp(startPosition, endTransform.position, time);
    if (time > 1) lerping = false;
}
void Update() {
    if (Input.GetKey("space")) StartLerp();
    UpdateLerp();
}

Exercise 1. Do a lerp!

After pressing a button once, lerp GameObject’s color from red to blue.

Bonus: After pressing twice, lerp the color back to red. Bonus bonus: What if you press the button during lerping?

Other interpolation functions

Custom interpolation

  • Lerping is a linear operation: the rate of change is constant during the process
  • Sometimes we want smoothing that is controlled more precisely than with SmoothStep and the like
  • Luckily, we can also create custom curves

Custom interpolation with an animation curve

  • for custom interpolation curves, use the AnimationCurve variable

    [SerializeField] AnimationCurve curve;

  • The curve can be manipulated in the inspector:

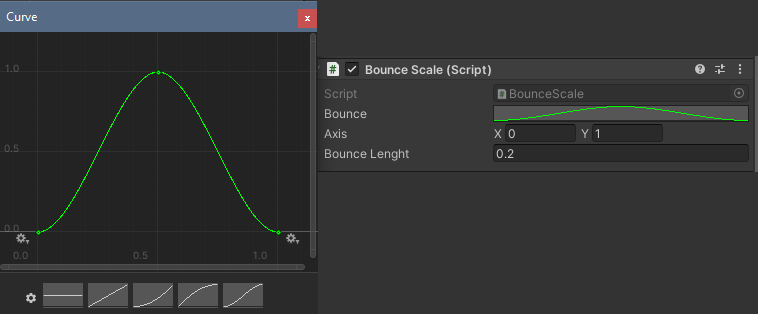
    • Click on the curve images on the bottom to choose and edit them

Controlling values with the curve

  • If the curve starts from 0 and ends in 1, you can use it as a replacement for Mathf.Lerp
    • If the curve starts from and ends in 0, you can create an animation that loops back to the initial value!
  • curve.Evaluate(t) returns a value from the graph (by default, between 0 and 1)
    • So we can lerp between a and b if we just supply this to a lerp function!
  • Mathf.Lerp(a, b, t) $\Rightarrow$ Mathf.Lerp(a, b, curve.Evaluate(t))

Animation curve example

public AnimationCurve bounce;
...

if(startTime > 0) // If we have set a startTime, do the interpolation
{
    // Calculate valid time for curve (between 0 and 1)
    float time = (Time.time - startTime) / bounceLenght;

    // Get the value from curve at the time of the animation
    // and multiply it with the desired scaled axis
    // then add it to default scale (1, 1, 1)
    transform.localScale = Vector2.one + axis * bounce.Evaluate(time);
}

Extra: Deltatime lerping on the fly

  • You may have seen lerp performed “on the fly” like this: 
    transform.position = Vector3.Lerp(transform.position, target.position, Time.deltaTime);
  • The start point changes every frame! And instead of a time parameter, there’s deltaTime…? What!?
  • This isn’t what lerp was meant to be used for, but this can be a useful trick
    • This creates a deceleration (“braking”) in the end which results in a smoother finish than lerp normally does (and it finishes faster than expected)
      • $\Rightarrow$ The interpolation isn’t linear anymore!
    • This is often used to make dynamic objects reach an end position gradually
      • Example: Camera that follows a bit behind the player character
  • There’s one important caveat, though…

Deltatime lerping is frame rate dependent!

  • This is bad! We get different results with different machines!
  • There’s a somewhat-known solution to this
    • Instead of 
      source = Mathf.Lerp(source, target, smoothing * Time.deltaTime);
    • Do this: 
      source = Mathf.Lerp(source, target, 1 - Mathf.Pow(smoothing, Time.deltaTime))
  • Read more here: Frame rate independent damping using lerp
    • In the link, there’s a techincal explanation why deltatime lerping works how it works, and why the solution above fixes the framerate dependence.

Slerp on-the-fly example

Vector3 relativePos = target.position + new Vector3(0,.5f,0) - transform.position;

transform.localRotation = 
  Quaternion.Slerp(
    transform.localRotation,
    Quaternion.Lookrotation(relativePos),
    Time.deltaTime
  );

transform.Translate(0,0, 3 * Time.deltaTime);

Extra: Inverse lerp

  • Script Reference: Inverse lerp
    • Mathf.InverseLerp(a, b, x)
    • Returns the answer to the inverse problem of Lerp:
      • “When we know a value $x$ that is between $a$ and $b$, what is $t$?”
      • In other words, how far is $x$ between $a$ and $b$, as a fraction

Extra: Remapping with lerp & inverse lerp

  • Freya Holmér: Inverse Lerp and Remap

  • What if we want to map a range $t_0 \dots t_1$ to range $a \dots b$?
  • Or in other words, map a variable input in range inputMin$\dots$inputMax
    • And get a result that is in a range outputMin$\dots$outputMax.
  • The function that achieves this is a sort of a “generalization” of lerp & inverse lerp: 
      float Remap (float inputMin, float inputMax, float outputMin, float outputMax, float input)
  {
      float t = Mathf.InverseLerp(inputMin, inputMax, input );
      return Mathf.Lerp( outputMin, outputMax, t );
  }
    • If input has the value of inputMin, the function returns the value outputMin.

Reading