1. Vectors

What is a vector?

Vector is a mathematical thingy with a length and a direction
Often represented by an arrow (see next slide)
Can have multiple dimensions (also called components)
- In our case usually 2 or 3:
- $x$, $y$, and possibly $z$
Video games are full of vectors!
- Used for depicting position, velocity, acceleration, forces….

2D vector example

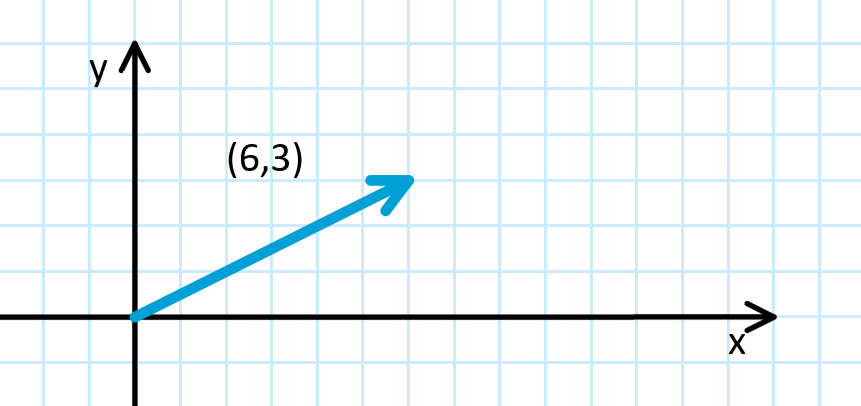
$bg right width: 90%$

This is a 2D vector $\vec{A} = (6, 3)$
- x-component $\vec{A}_x = 6$
- y-component $\vec{A}_y = 3$
Vectors start from the origin, or $(0,0)$
In C#:
```
Vector2 vectorA = new Vector2(6,3);
```

2D vector length

The length of a 2D vector is given by the Pythagoras theorem
- $ \vec{A} = \sqrt{\vec{A}_x^2 + \vec{A}_y^2}$
- $ (6,3) = \sqrt{6^2 + 3^2} = \sqrt{36 + 9} = \sqrt{45} \approx 6.7$

In C#:

float length = Mathf.Sqrt(Mathf.Pow(vectorA.x, 2) + Mathf.Pow(vectorA.y, 2));

Vector classes have a shorthand, too: A.magnitude

Vector arithmetic

Manual: Understanding Vector Arithmetic
Let’s introduce the most important vector operations
- Addition
- Subtraction
- Scalar multiplication
- Extra: vector multiplication
  - Dot product
  - Cross product (WIP)
C# examples included

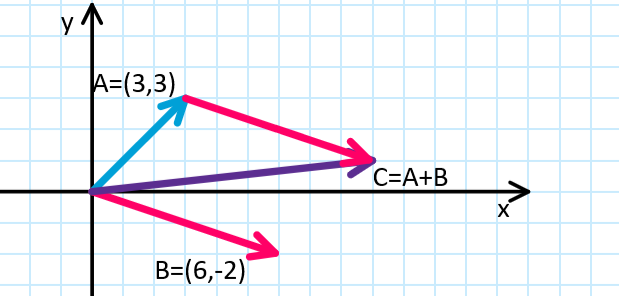
Vector addition

sum of two vectors is calculated by summing up the individual components
$\vec{C} = \vec{A} + \vec{B}$ $= (3, 3) + (6, -2)$ $= (3 + 6, 3 - 2) = (9, 1)$

can be illustrated by moving $\vec{B}$ to start from the endpoint of $\vec{A}$

Vector2 A = new Vector2(3.0f, 3.0f);
Vector2 B = new Vector2(6.0f,-2.0f);
Vector2 C = A + B;

$bg right width: 90%$

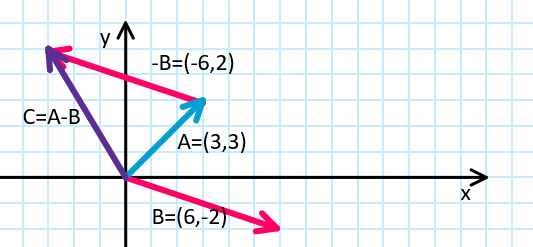
Vector subtraction

difference of two vectors, $\vec{A} - \vec{B}$
- $-\vec{B}$ is is “flipped” $\vec{B}$: $\vec{B} = (6, -2) \Rightarrow -\vec{B} = (-6, 2)$
- $\vec{C} = \vec{A} - \vec{B}$ $= (3, 3) - (6, -2)$ $= (3 - 6, 3 - (-2))$ $= (3 - 6, 3 + 2)$ $= (-3, 5)$

$\vec{A} - \vec{B}$ starts from the endpoint of $\vec{B}$ and ends in the endpoint of $\vec{A}$

Vector2 A = new Vector2(3.0f, 3.0f);
Vector2 B = new Vector2(6.0f,-2.0f);
Vector2 C = A - B;

$bg right:40% width: 90%$

Scalar multiplication

When a vector is multiplied by a scalar (a number), the vector is scaled
- If a vector is multiplied by 2, its length doubles $2 \cdot \vec{A}$ $= 2 \cdot (3,2)$ $= (2 \cdot 3, 2 \cdot 2)$ $= (6, 4)$
```
Vector2 A = new Vector2(3.0f,3.0f);
Vector2 C = 2 * A;
```

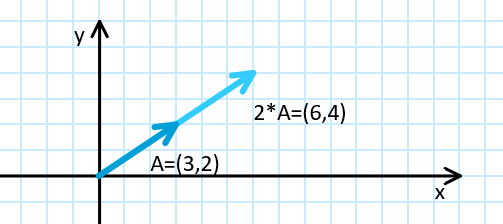
$bg right:40% width: 90%$

Special cases for scalar multiplication

If the scalar is negative, the vector gets flipped
- that’s what happened in subtraction
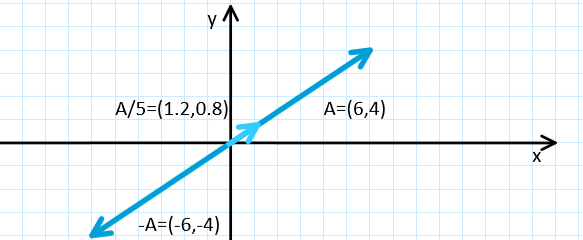
- $-\vec{A} = -1\cdot \vec{A} = -1 \cdot (6,4) = (-1 \cdot 6,-1 \cdot 4) = (-6, -4)$
What about division?
- it’s basically multiplication as well
- $\vec{A} / 5 = \frac{1}{5} \cdot \vec{A} = \frac{1}{5} \cdot (6,4) = (\frac{1}{5} \cdot 6,\frac{1}{5} \cdot 4 ) = (\frac{6}{5},\frac{4}{5} ) = (1.2, 0.8)$

Vectors in Unity

Vectors in video games

position
velocity
acceleration
rotation
forces

Vector classes

Unity has two Vector classes, Vector2 and Vector3
- “2” and “3” here are the number of dimensions: (x,y) and (x,y,z)
- ```
  Vector2 position = new Vector2(1.0f, 2.0f)
```
Vector components can be accessed with the dot notation:
- position.x, position.y, position.z
Vectors can’t be directly modified:
- No: position.x = 3.0f
- ```
  position = new Vector2(3.0f, position.y);
```
Length of a vector can be acquired with vector.magnitude
- Script Reference: Vector3 magnitude

Velocity vector

Velocity is an important concept in game development!
It’s the rate of change of position
- new_position = old_position + velocity;
3-dimensional velocity vector can be added like this to GameObject’s position in an Update() method:
- transform.position += velocity;
- We can use player input, collision, etc. to adjust the velocity as needed
  
  Note: Velocity vector is usually drawn so it starts from the moving object
- (Remember, though, that vectors do not “know” its starting positions.)

Acceleration vector

Another important concept is acceleration
It’s the rate of change of a GameObject’s velocity!
- new_velocity = old_velocity + acceleration;
We can use acceleration to change Rigidbody’s velocity
- rb.velocity += acceleration;
We can’t use that for GameObjects without rigidbodies, but we can store velocity in a separate variable
```
velocity += acceleration;
transform.position += velocity;
```
This might seem like a cheap trick, but actually allows us to create smoother motion if we use player input, collision, etc to control acceleration instead of velocity

Distance vector

To get the distance vector between two objects, we use vector subtraction
- vector_B - vector_A
- transform.position - otherGameObject.transform.position;
To just get the length of the distance vector, a.k.a, the distance:
- Vector2.Distance(vector_A, vector_B)

Special vectors of Unity

See Static properties in Script Reference: Vector3
- Vector3.right: the global $x$ axis
- Vector3.up: the global $y$ axis
- Vector3.forward: the global $z$ axis

Common vector operations

Normalizing a vector

When we are not interested about the length of a vector, only its direction, it helps to normalize the vector
Normalizing means setting the length of a vector to be $1$
This is achieved by dividing the vector by its length
$\vec{A}_{normalized} = \vec{A} / \vec{A} $
in C#, the normalized version of any vector can be easily accessed:
```
Vector2 UnitVector = A.normalized;
```

Rotating a vector

In Unity, rotation is represented by Quaternions (fin. kvaternio, kvaterniot)
To rotate a vector by a given angle, you can do a Quaternion rotation operation:
```
Vector3 rotatedVector = Quaternion.Euler(0, 0, 90) * originalVector;
```
- This isn’t a regular multiplication, so do note that Quaternion.Euler has to be on the left side of the vector.

To rotate a Quaternion:

myQuaternion *= Quaternion.Euler(0, 0, 90);

Note: the Transform and Quaternion classes have many rotation methods available, see Transform Class: Rotation

Extra: Dot product - Vector’s alignment with another vector

If you want to know how much two vectors point to the same direction, we can use the dot product
- Script Reference: Vector3.Dot
The dot product returns a number, not a vector!
- $\vec{A} \cdot \vec{B} = A_{x} \cdot B_{x} + A_{y} \cdot B_{y} + A_{z} \cdot B_{z}$
For normalized vectors, Vector3.Dot returns
- $1$ if they point in exactly the same direction
- $-1$ if they point in completely opposite directions
- $0$ if the vectors are perpendicular

Dot product example

Check if two rigidbodies are moving to the same direction:

float alignment = Vector3.Dot(
  _rigidBody.velocity.normalized,
  otherGameObjectRigidBody.velocity.normalized)

Note about distance

Note: when performance is important, using magnitude can be a bad idea: it includes the costly square root operation
- if you need to only compare magnitudes, or you’re squaring it right away, use .sqrMagnitude instead!

Exercise 1. I’m being avoided

Create a scene with two GameObjects, a player and a static enemy. Calculate the distance between the player and the enemy.

If the distance is smaller than some given threshold value,

⭐ Change the color of the enemy (and set the color back to default when you’re no more on the range)
⭐⭐ Make the enemy shoot at player!
⭐⭐⭐ Move the enemy farther away from the player along the shortest possible path.

Math 1. Vectors